Discrete Mathematics 1

A total of almost 61 hours of lectures

This is the first part of our series of three courses in Discrete Mathematics. It can be seen as a bridging course from high school to university mathematics, as it lays the foundation for all future maths courses, teaches you the basics of mathematical reasoning, and the main proof techniques.

Image precalculus part 1

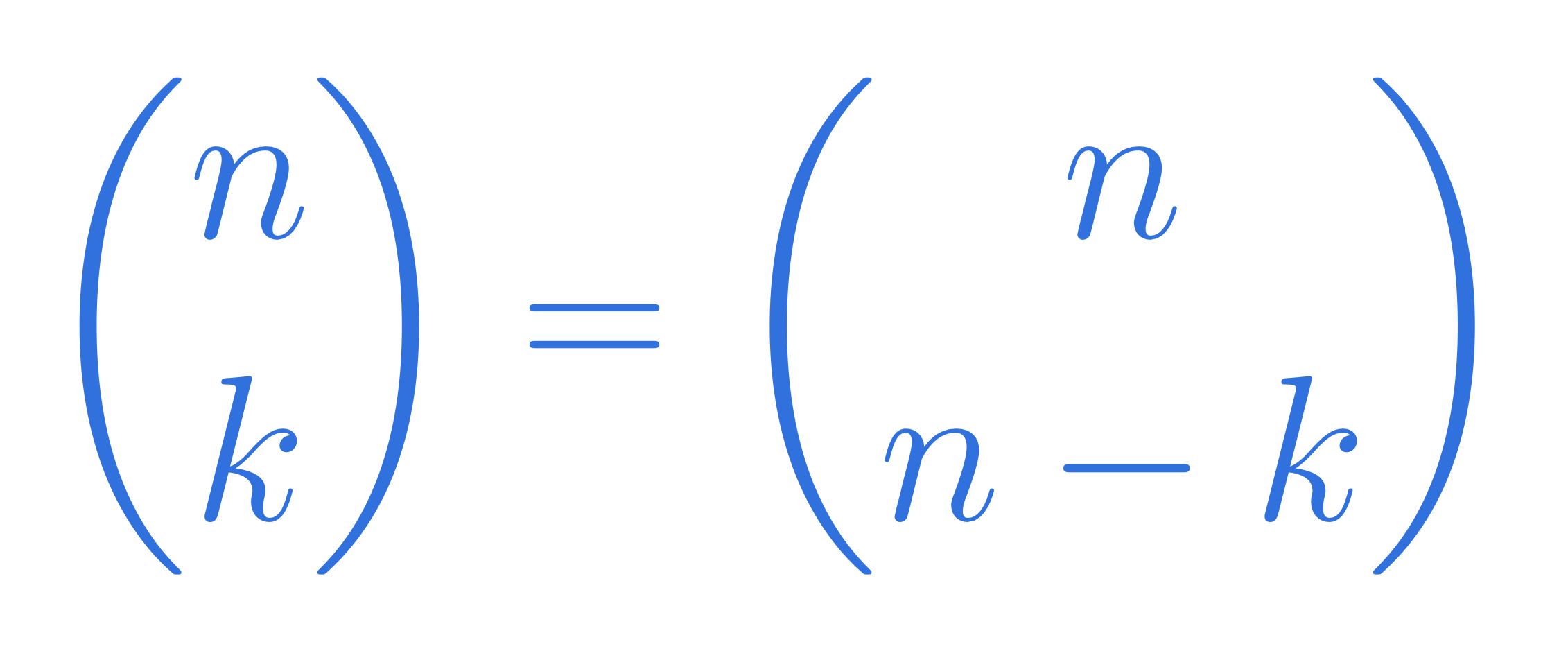
Prerequisites

High-school maths, mainly arithmetics.

Curriculum

Make sure that you check with your professor what parts of the course you will need for your exam. Such things vary from country to country, from university to university, and they can even vary from year to year at the same university.

Discrete Mathematics 1

h

Get the outline

A detailed list of all the lectures in part 1 of the course, including which theorems will be discussed and which problems will be solved. If you are looking for a particular kind of problem or a particular concept, this is where you should look first.

Get Discrete Mathematics 1 on Udemy

When you buy the course on Udemy, you get access to it for life. There is just a one-time fee. The prices do vary a lot on Udemy, but if you use our link by clicking on this panel, you will get the best current price. See also our page on “coupon codes” in the menu (the current code is TPOT_OCT26).

Course Objectives & Outcomes

Z
How to solve problems in chosen Discrete-Mathematics topics (illustrated with 395 solved problems) and why these methods work, step by step.
Z
Elementary Set Theory, including working with intersections and unions of sets, and other set-related topics.
Z
The concept of function between two discrete sets: injections, surjections, bijections.
Z
RST relations and the concept of equivalence classes; an illustration for a modulo relation between integers.
Z
An introduction to the topic of sequences, only basic concepts that can be needed in Combinatorics; we come back to the topic of sequences in DM3.
Z
A preparation for Combinatorics: the concept of index, the sigma sign (with computational rules), n factorial, n choose k, Pascal’s Triangle, Binomial Theorem.

Z
Playful logical problems and riddles, including the famous Zebra Puzzle (Einstein’s Riddle), and some classical riddles about liars and truth tellers.

Z
Elementary Logic, including proving tautologies that involve implications, conjunctions, and disjunctions; necessary and sufficient conditions.
Z
An introduction to mathematical theories, with concepts like axiom, theorem, primitive notion, etc.

Z
The concept of (a binary) relation as a subset of Cartesian product of two sets: RST relations, order relations, etc.
Z
Functions as relations; various ways of depicting functions between two discrete sets; equipotent sets.

Z
Various proof techniques, including direct proofs, proofs by contradiction, proofs by contrapositive, Mathematical Induction, and Pigeonhole Principle.
Z
A brief introduction to Combinatorics: the art of counting. Permutations, combinations, paths, etc; the topic will be continued in the first sections of DM2.
Z
This is the first course in Discrete Mathematics, so don’t worry that neither Number Theory nor Graph Theory are covered; they will be covered in a sequel.
Francisco O.
Udemy student
Once again another fantastic course, it begins slowly but it ends with a nice but challenging introduction to combinatorics
Varga-Henn M.
Udemy student
Well detailed introduction!
Pierpaolo D.
Udemy student
Thanks Hania for the great course!!
Stephen P.
Udemy student
Our professor is extremely clear and realistic about the objectives of this course and I am beyond excited. Her response time to messages is unrivaled.
Jerry K.
Udemy student
The way it was presented and explained was completely understandable and applicable to me. I often need additional examples for explanations to get a full understanding but I did not need to seek additional information while listening to these videos
Łukasz D.
Udemy student
NIc dodać nic ująć.Machine translation: Nothing more, nothing less.
Lionnel M.
Udemy student
Very good
John H.
Udemy student
Hania, has or will soon have 13 courses on Udemy. They are excellent prep for Engineering or any STEM degree. I would recommend any high school student planning on a STEM degree, review as many of her courses as possible, before first year. She breaks the subject matter down and thoroughly explains it.
Nomboh Q.
Udemy student
really interesting and i love the way she teaches
Leviathan G.
Udemy student
Very detailed and organized. I’m excited to begin learning.
More reviews (35)